Best Of The Best Tips About How Can A Graph Be Simple Make In Excel From Data

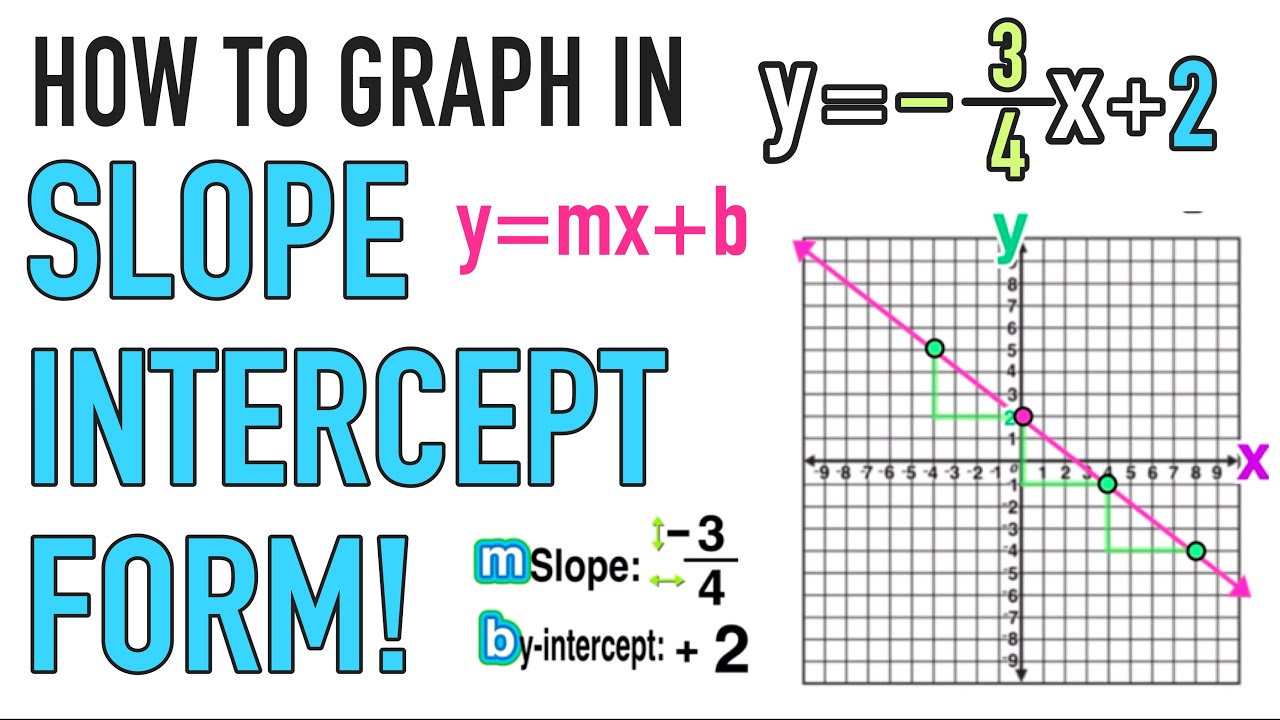
This article explores a simple graphing method that can be used to approximate solutions to equations that cannot be solved directly.

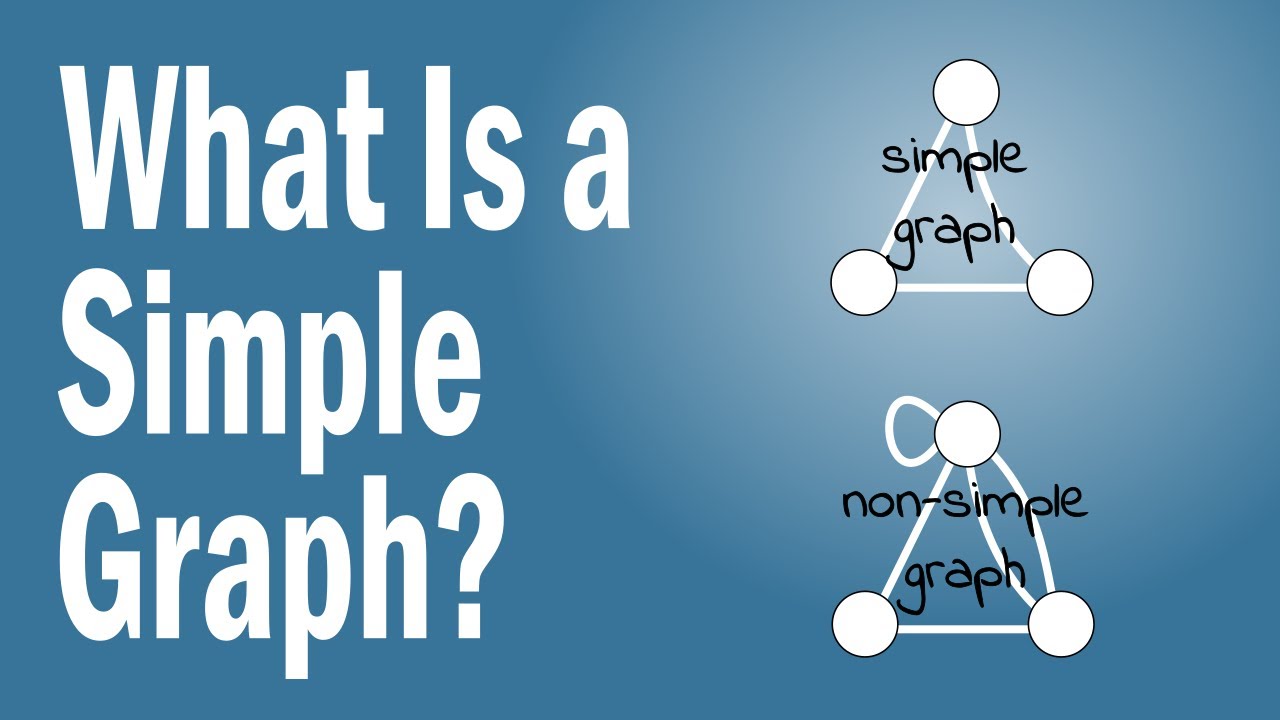
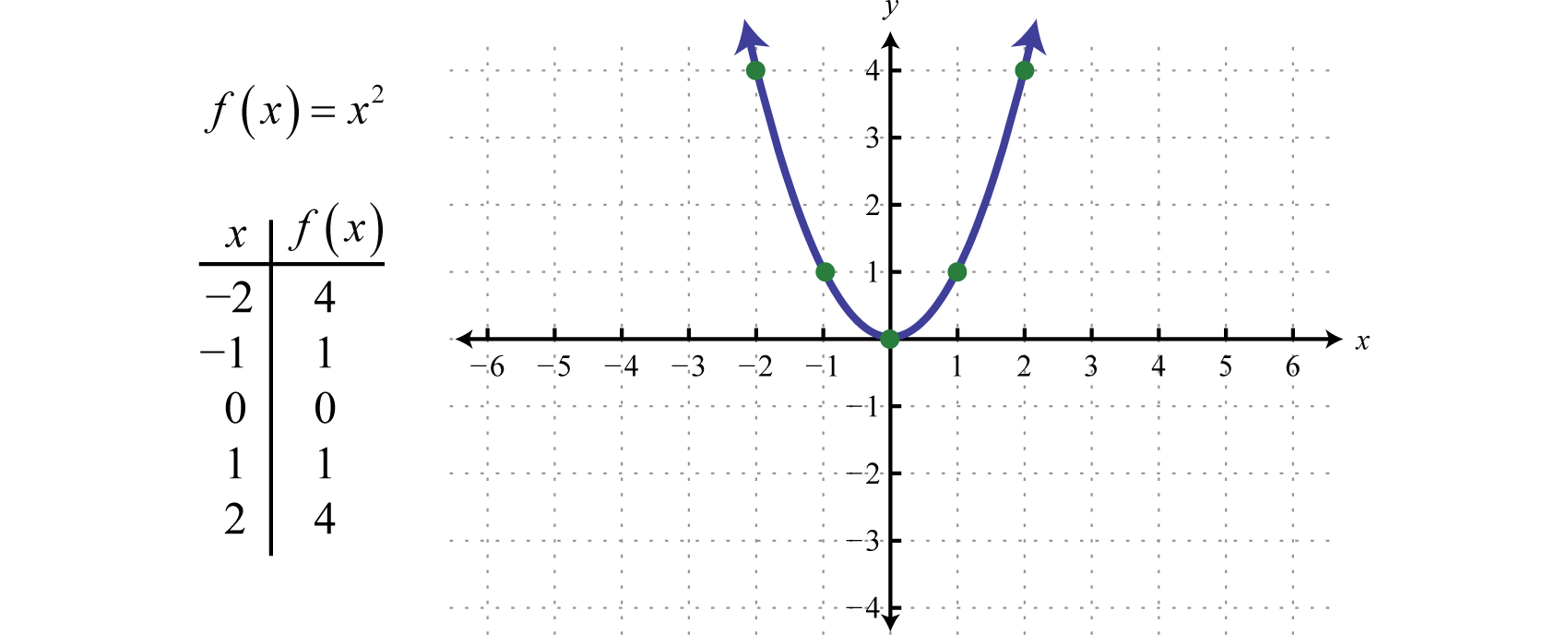
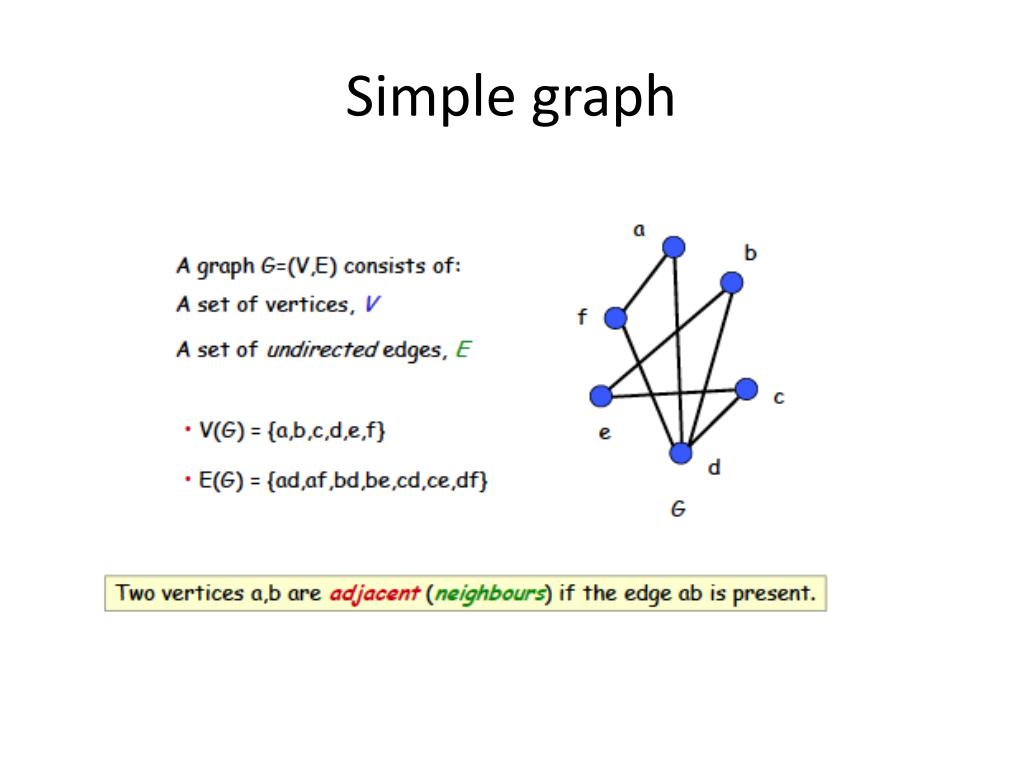
How can a graph be simple. Let g g be a simple graph. To sum up, a simple graph is a collection of vertices and any edges that may connect them, such that every edge connects two vertices with no loops and no two vertices are. It is stated by wikipedia as:

In set terms, this graph is. How many refugees are there around the world? To represent an edge, we just have an array of two vertex numbers, or an.

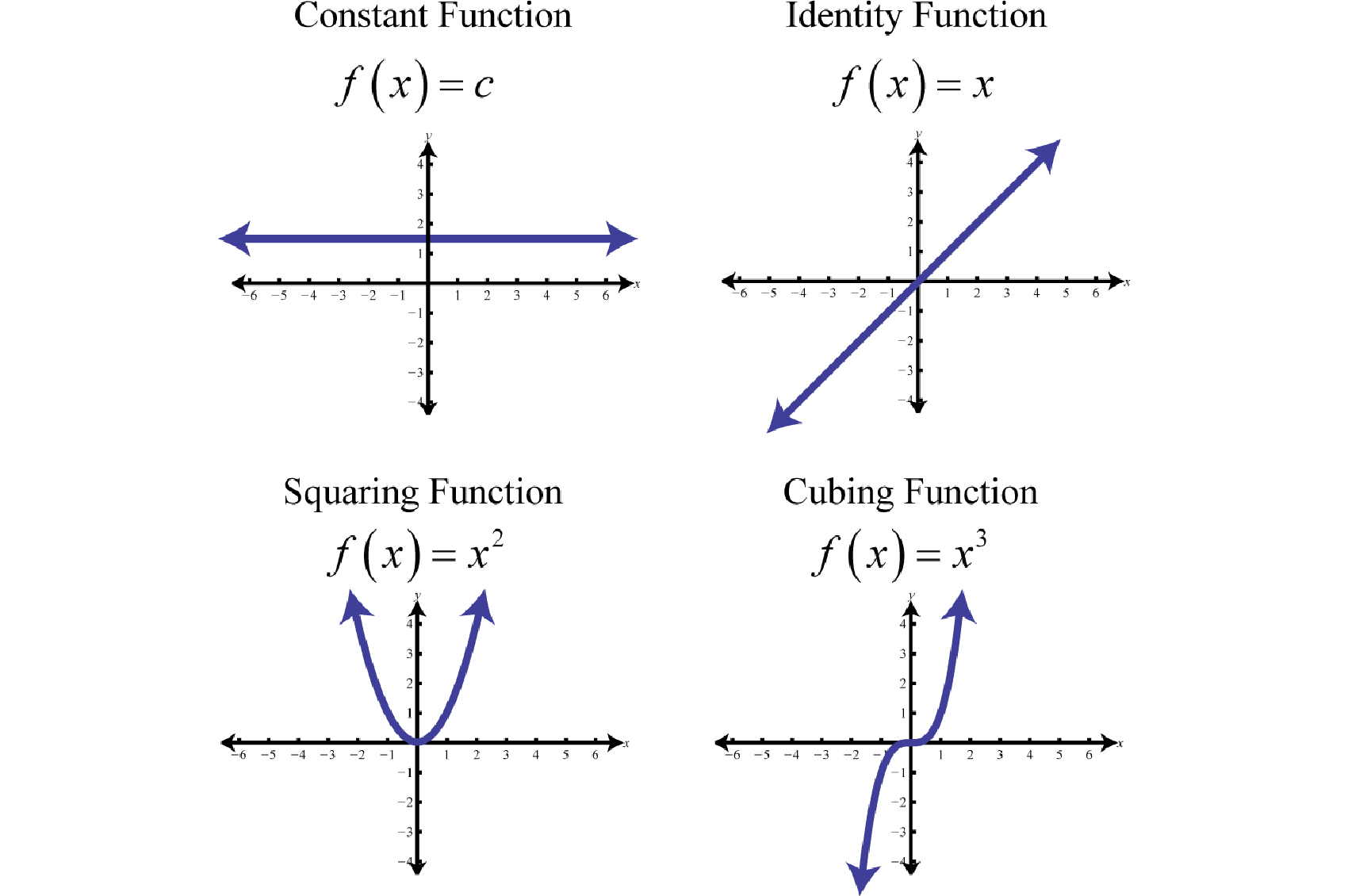
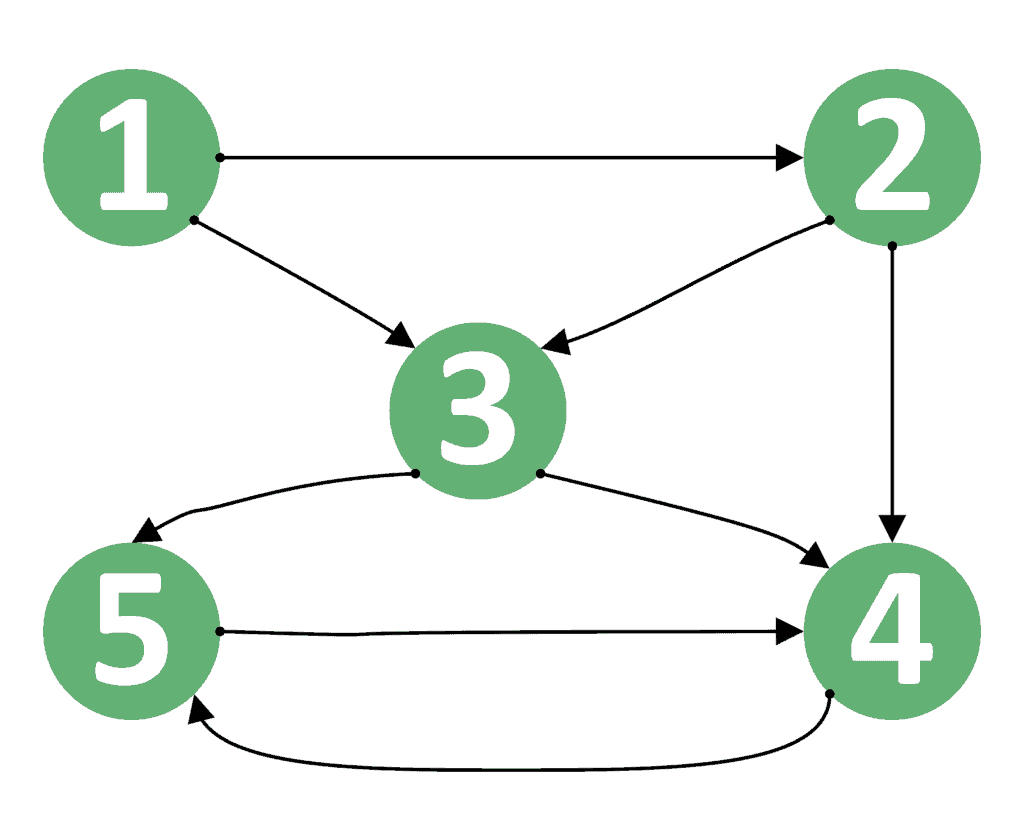
Figure \(\pageindex{1}\) is an example of a simple directed graph. In other words a simple graph. A simple graph is a graph that does not contain more than one edge between the pair of vertices.

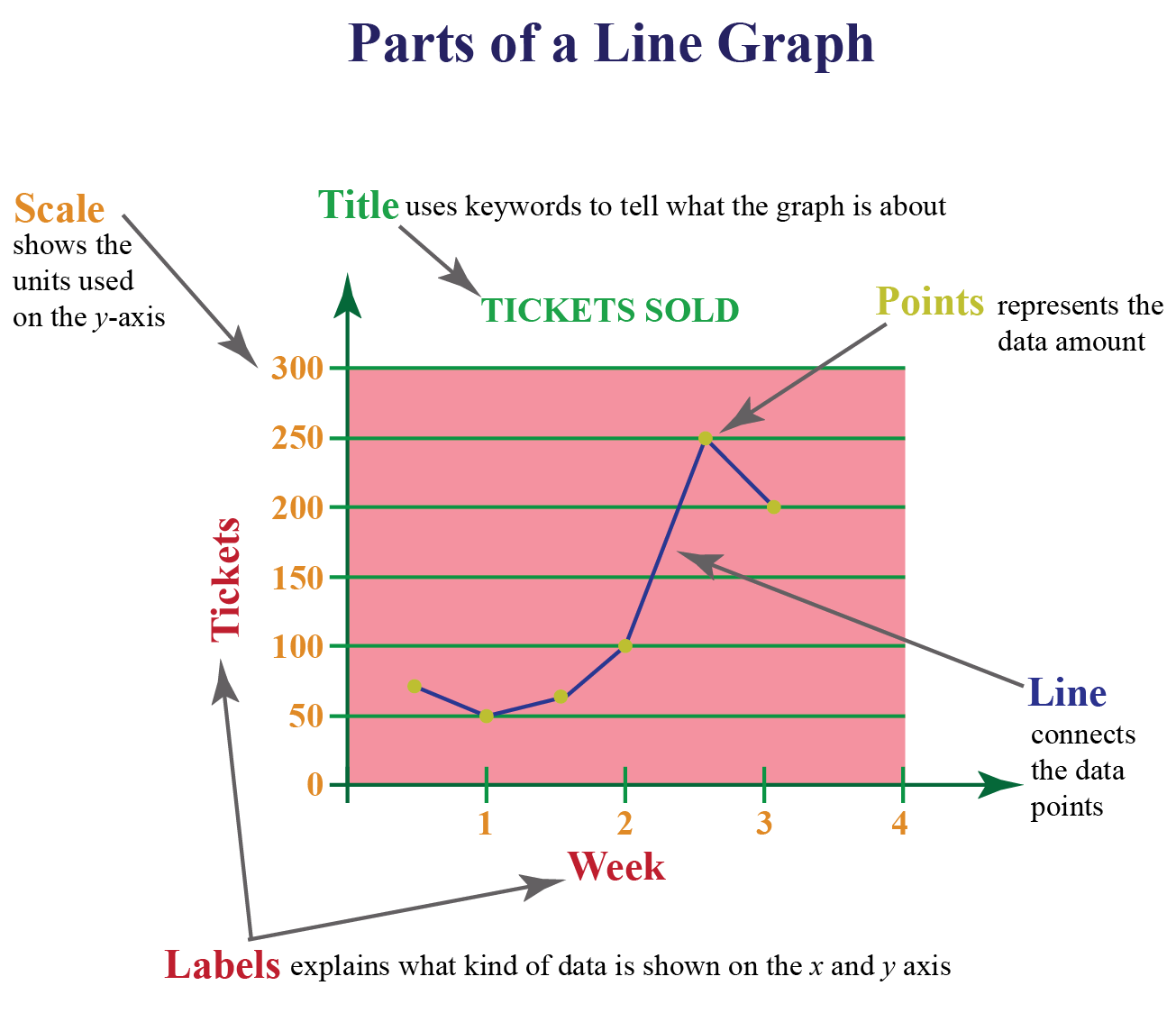
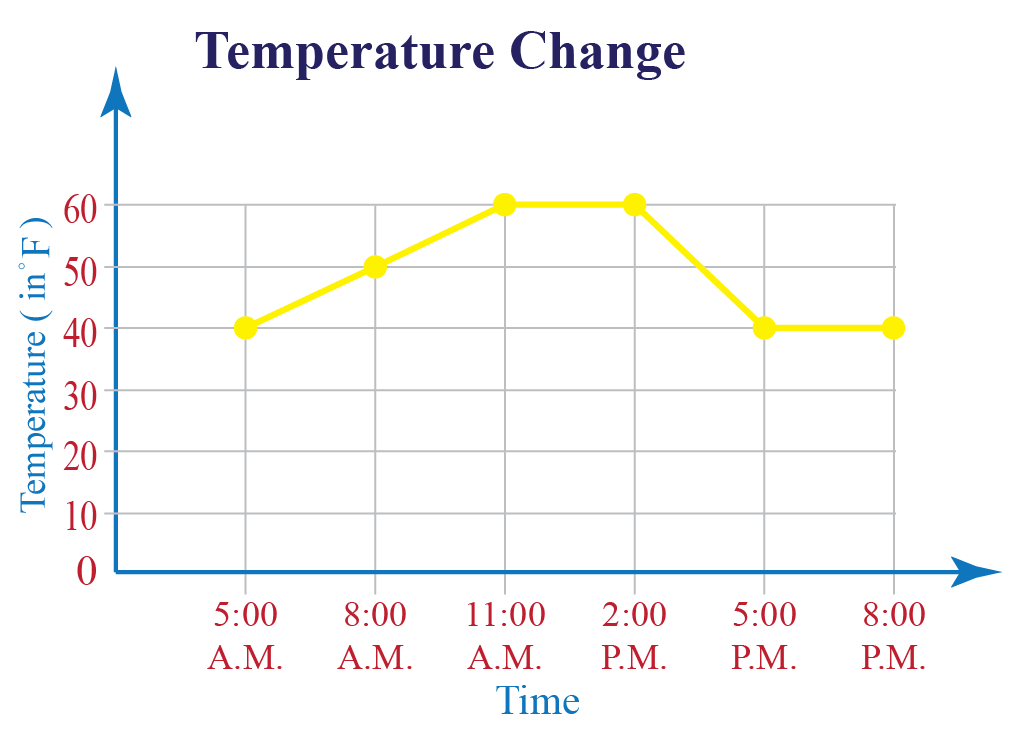
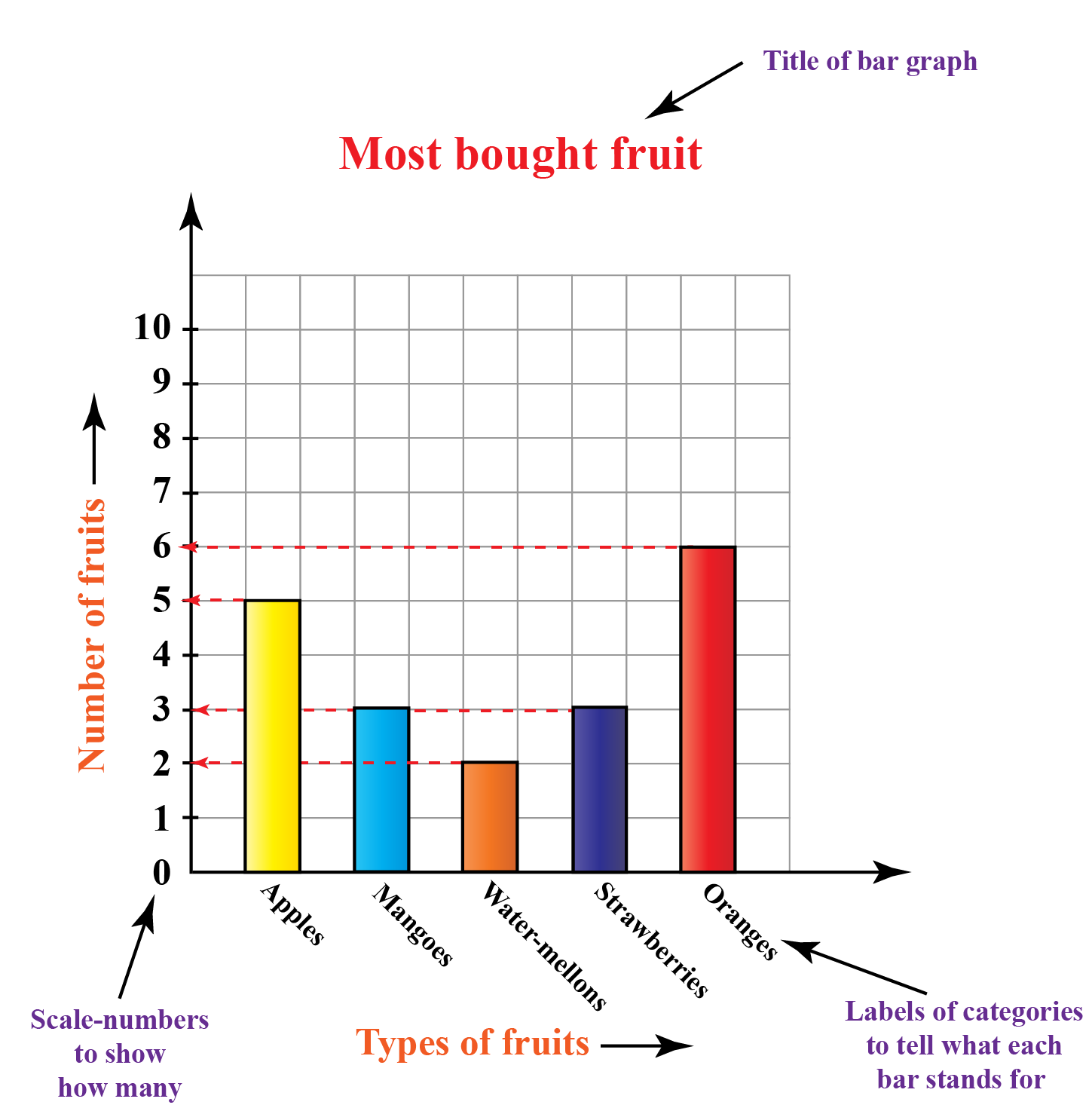
An element of v.g/ is called. At least 117.3 million people around the world have been forced to flee their homes. A graph can be defined as a diagram representing relation between variable quantities or data in an organized manner.

The maximum number of edges possible in a single graph with ‘n’ vertices is n c 2 where n. A graph with no loops and no parallel edges is called a simple graph. It’s used to represent relationships between different entities.

Each line is an edge, connecting two vertices. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. A simple graph is a graph that does not have more than one edge between any two vertices and no edge starts and ends at the same vertex.

A simple graph is a graph that does not contain any loops or parallel edges. If we want to use a graph in python, networkx is probably the most popular choice. Explore math with our beautiful, free online graphing calculator.

This video explains what a simple graph is and shows why this type of graph is so widely used. The edges of a simple graph can be represented as a set of. Thus, $v_3$ must be adjacent to.

Because the know each other relationship goes both ways,. To sum up, a simple graph is a collection of vertices and any edges that may connect them, such that every edge connects two vertices with no loops and no two vertices are. Among them are nearly 43.4 million.

If the graph is simple, and $\deg v_1=3$, $v_1$ must be adjacent to each of the other three vertices. We denote an edge connecting vertices u and v by the pair ( u, v). The video contains an example and exercises to practice this.d.