Favorite Info About How Do You Describe A Linear Plot Line Graph Does Not

A quick description of the association in a scatterplot should always include a description of the form, direction, and strength of the association, along with the presence of any outliers.

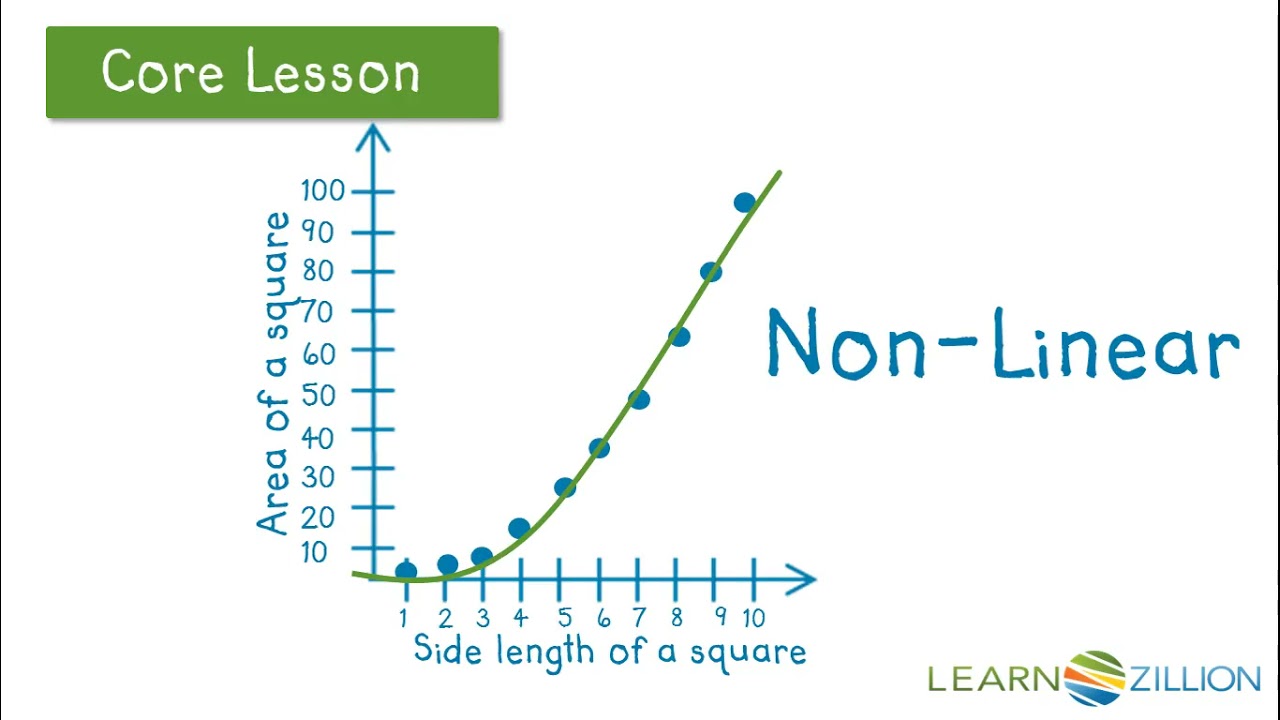
How do you describe a linear plot. Scatter plots are used to observe relationships between variables. A scatterplot is also known as a scatter diagram. A scatterplot is used to visualize a relationship between datasets, enabling you to interpret whether there is a trend in your data or not.

This graph helps in depicting a result in single straight lines. With regression analysis, you can use a scatter plot to visually inspect the data to see whether x and y are linearly related. Match linear functions with their graphs.

I could think of the following options: The scatter plot is used to visually identify relationships between the first and the second entries of paired data. Find the equations of vertical and horizontal lines.

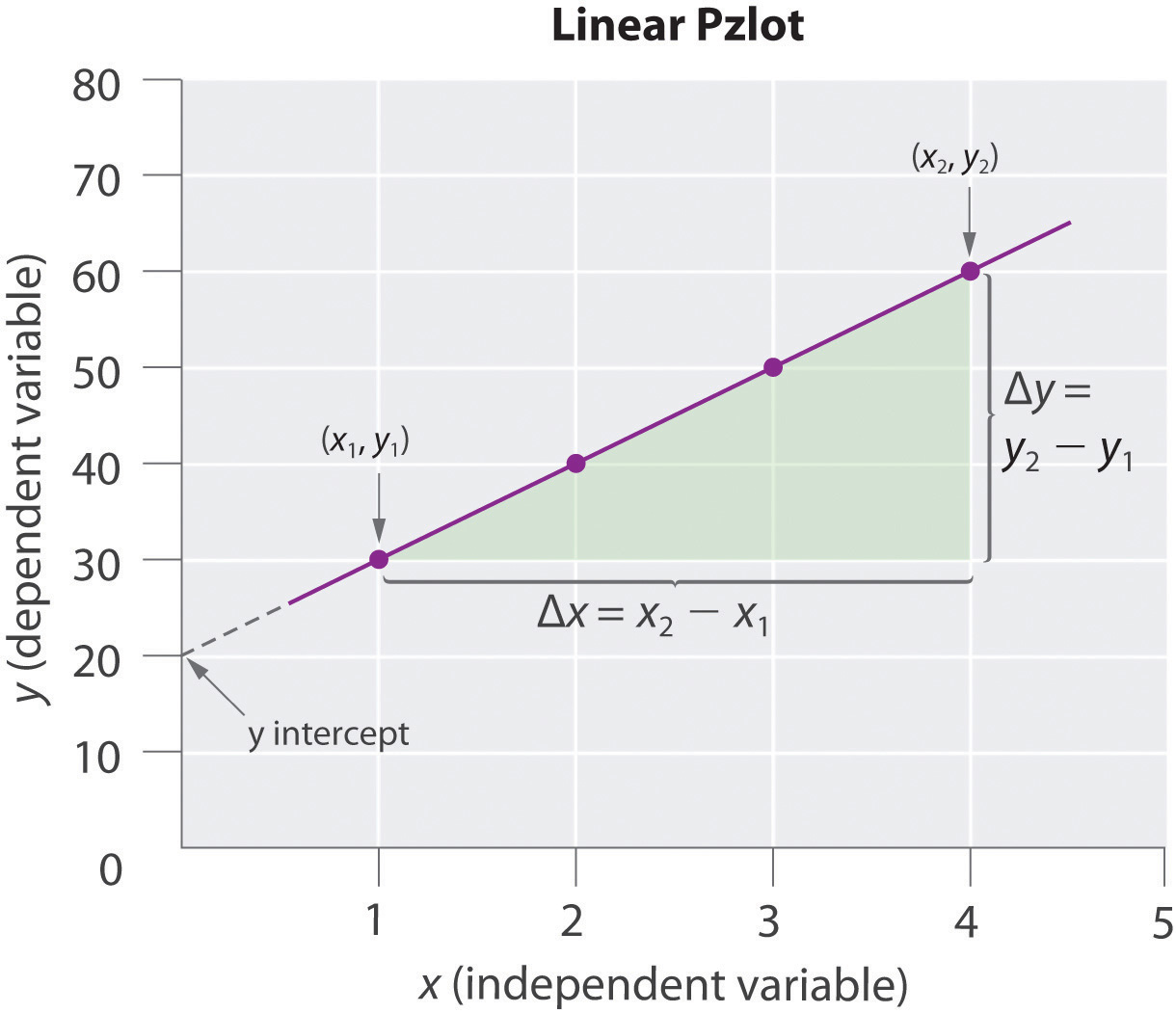
Scatterplots show possible associations or relationships between two variables. Linear graphs compare these two variables in a vertical axis and a horizontal axis. The horizontal axis depicts a continuous progression, often that of time, while the vertical axis reports values for a metric of interest across that progression.

Each member of the dataset gets plotted as a point whose ( x, y) coordinates relates to its values for the two variables. When we look at a scatterplot, we should be able to describe the association we see between the variables. Whatever the pattern is, we use this to describe the association between the variables.

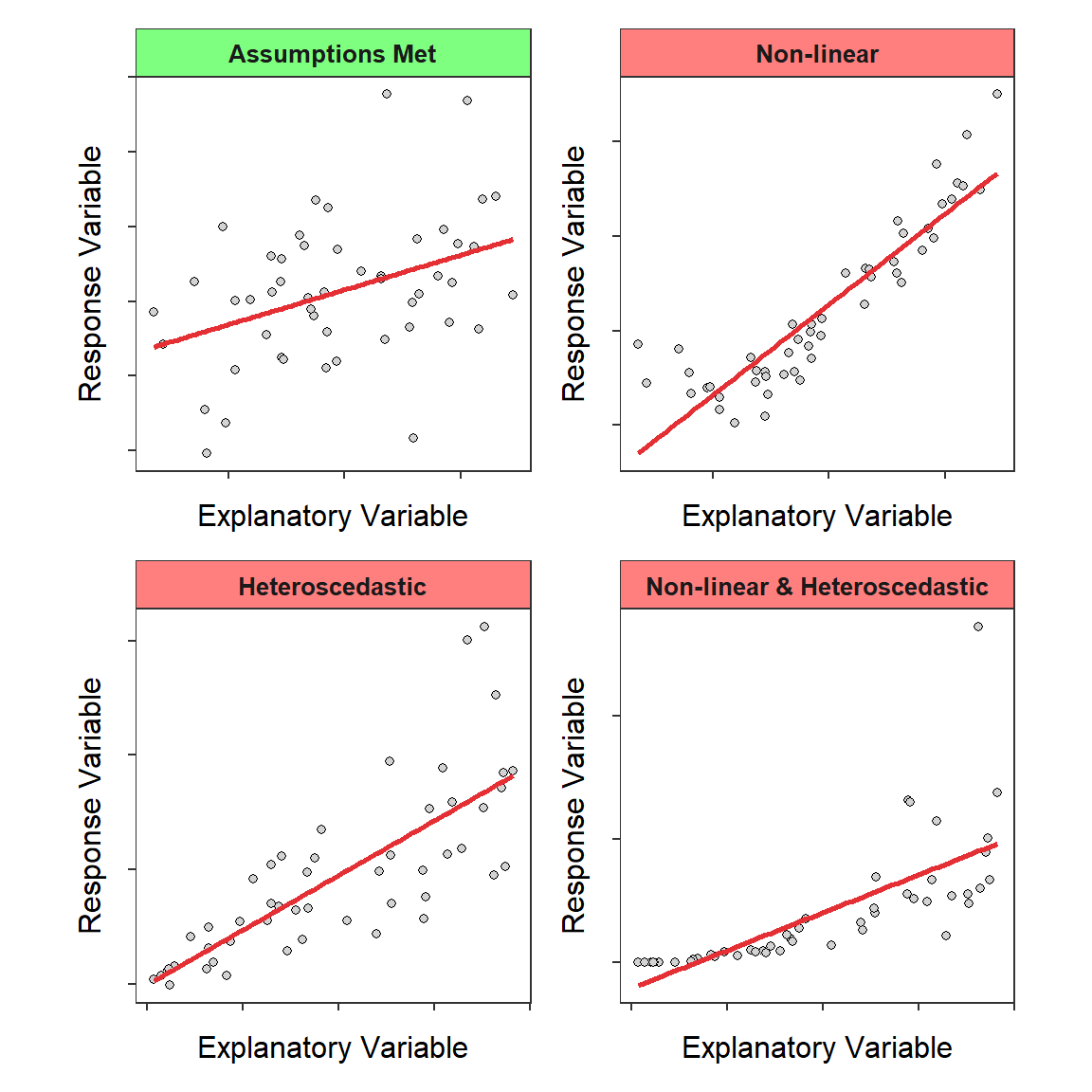
A scatter plot is a plot of the dependent variable versus the independent variable and is used to investigate whether or not there is a relationship or connection between 2 sets of data. A scatterplot is a type of data display that shows the relationship between two numerical variables. Describe any trend in the data, in terms of form, direction, strength, and outliers.

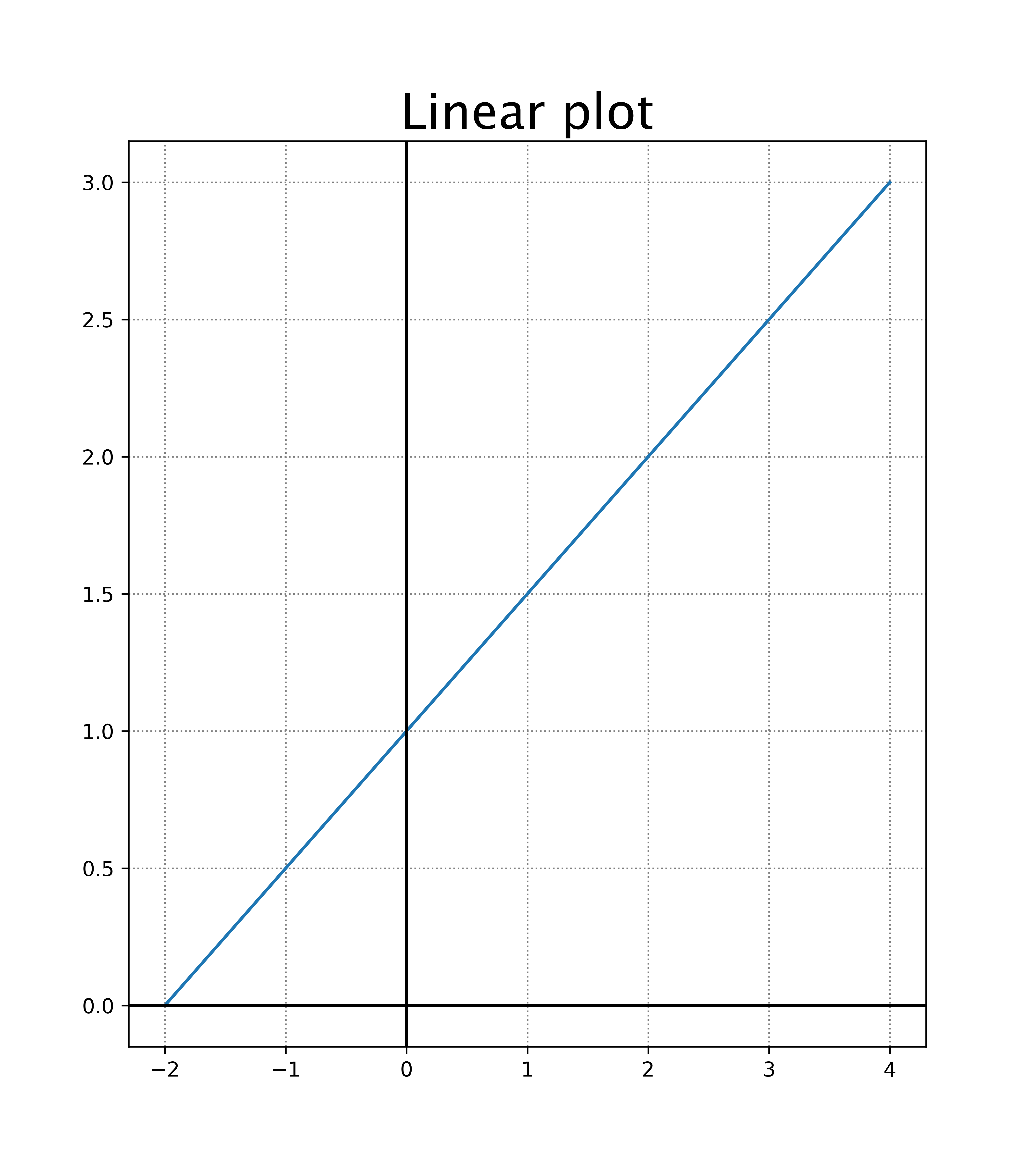
Ax + by = c, for some real numbers a, b, and c where a and b, are not 0. The following are some examples. Graphs of two or more straight lines can be used to solve simultaneous linear equations.

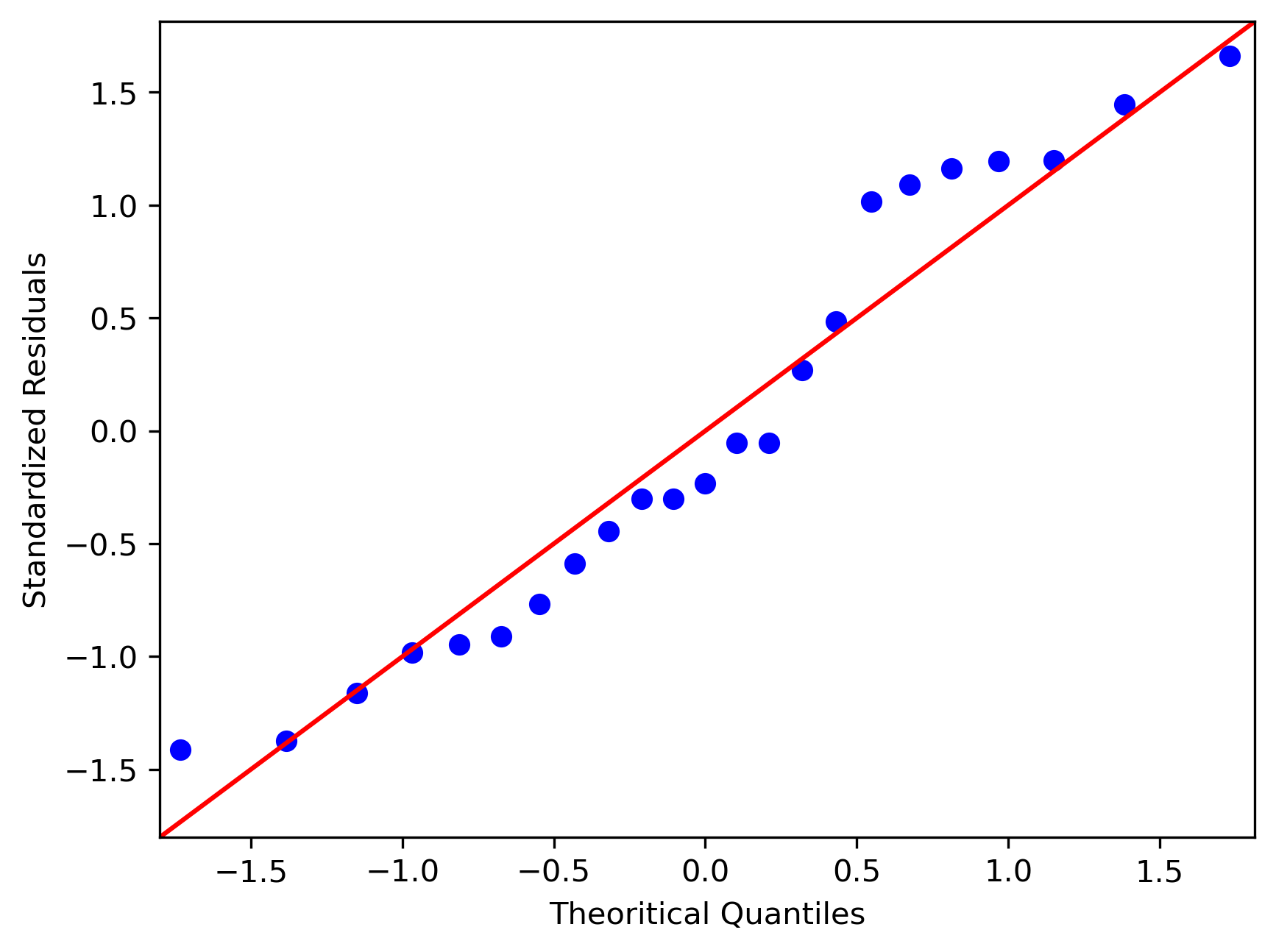
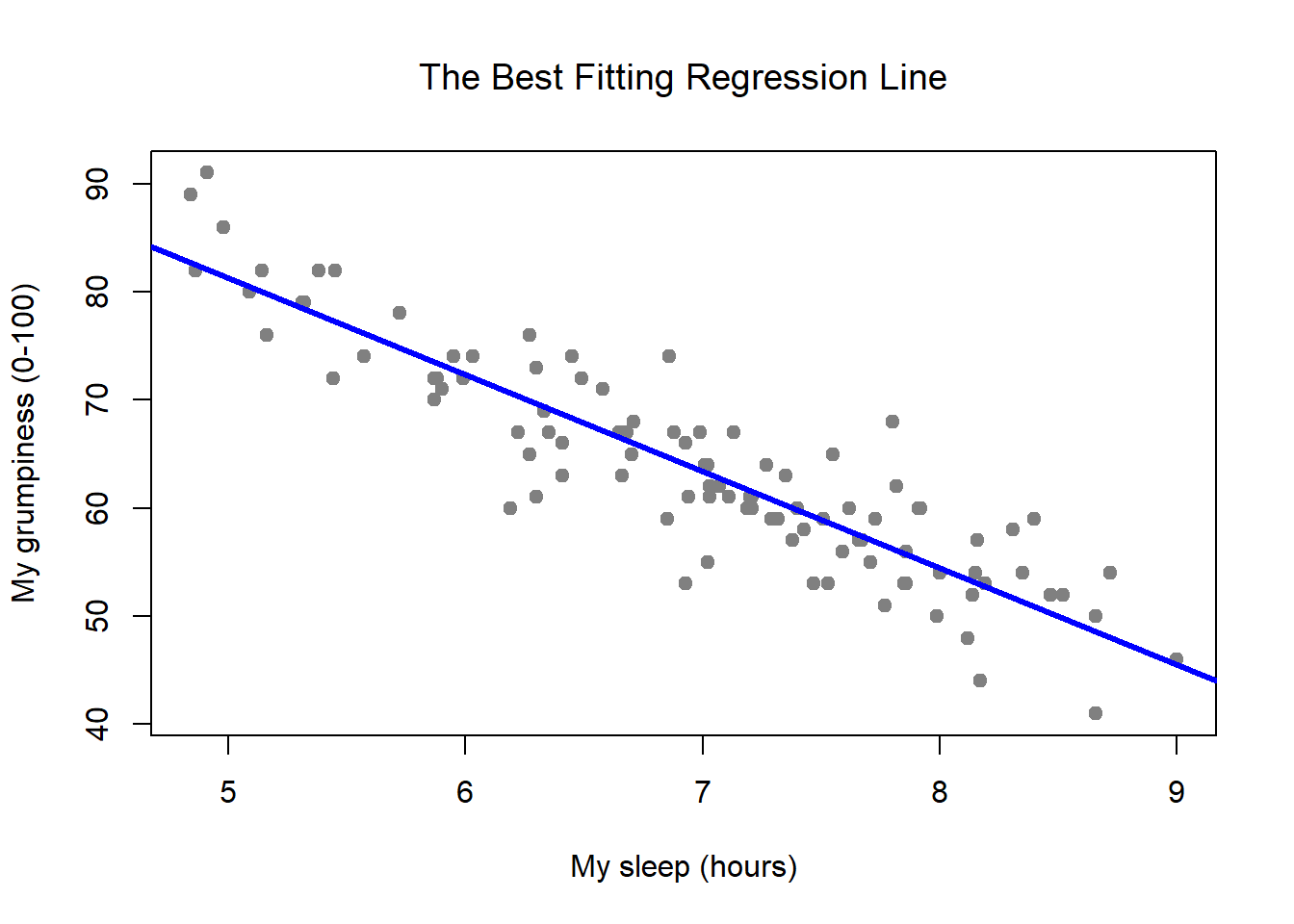
The scatter plot above represents the age vs. The 3 dots above 21 mean that 3 turtles traveled a distance of 21 meters in an hour. Mention the regression equation as described in (i) ( i) (coefficients, constant) along with standard deviation and then a residual error plot to show the accuracy of this model.

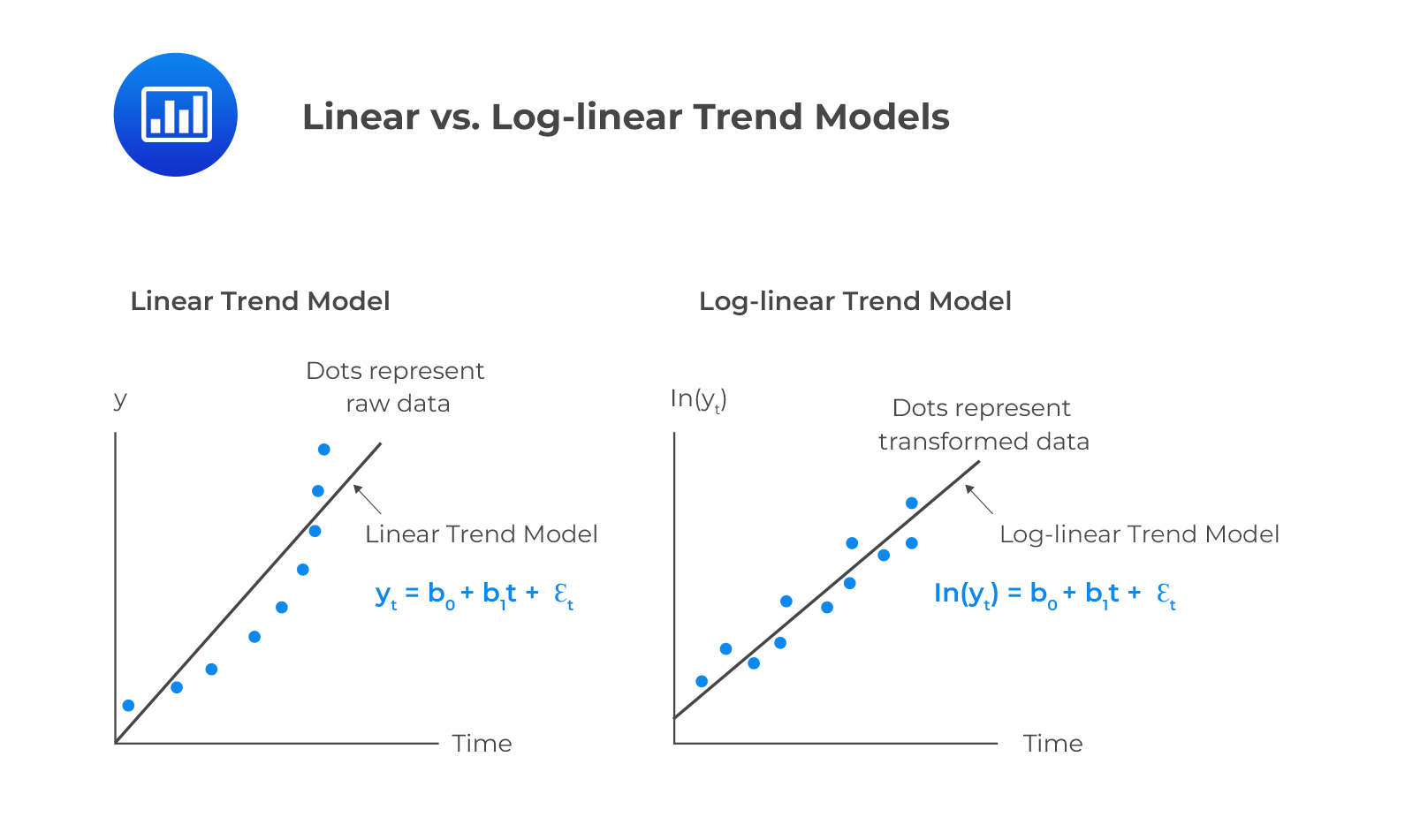
A linear equation is an equation that can be written in the form: Form, direction, strength, and outliers. Step length, turning angle or a spatial feature) takes the form η it = f x it $$ {\eta}_{it}=f\left({x}_{it}\right) $$.

Slope a line can have positive, negative, zero (horizontal), or undefined (vertical) slope. The scatterplot appears to have a roughly linear relationship, as opposed to a parabolic, or other relationship. It is clear from the scatter plot that as the plant ages, its size tends to increase.