Fantastic Tips About What Is Smooth In Math Ggplot Horizontal Bar

Smooth function, a function that is infinitely differentiable;

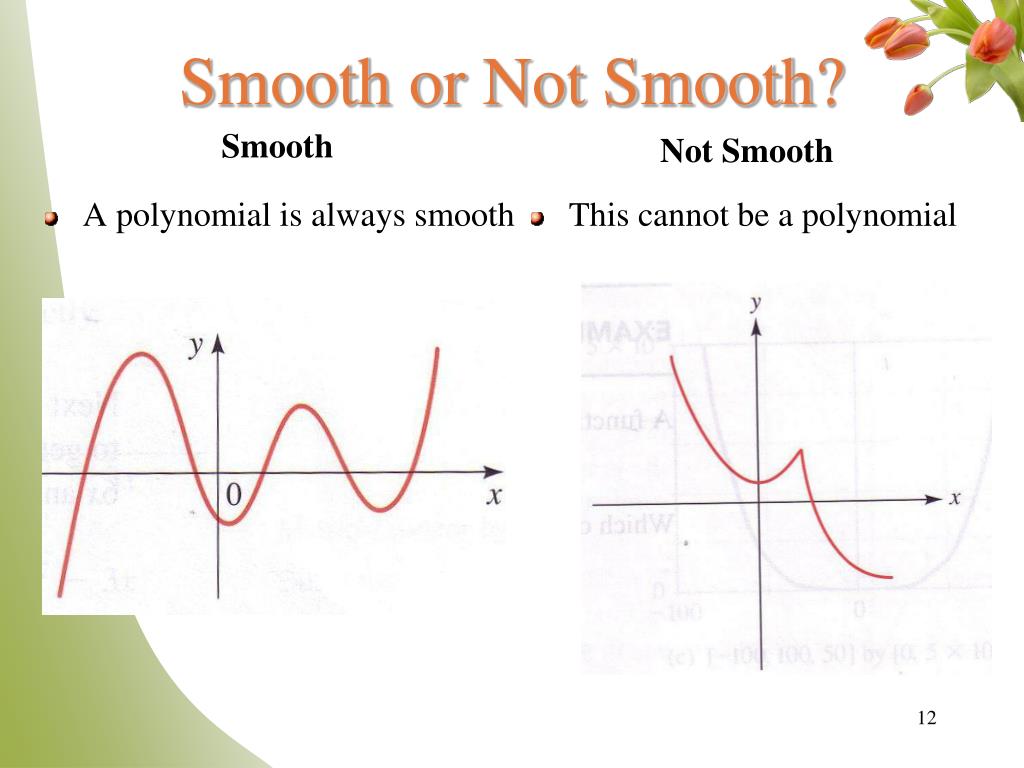
What is smooth in math. A smooth function can be discontinuous. In this video, i define what it means for a function to be smooth, as well as what being of order k means. Smooth functions have a unique defined first derivative (slope or gradient) at every point.

Highlights develop efficient methods for. [ a, b] → c. Used in calculus and topology.

In particular, a smooth curve is a. [a, b] → c ϕ: A path ϕ ϕ is a continuous mapping from a segment of the real axis into the complex numbers;

A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. A path ϕ ϕ is smooth if it is a differentiable. Is the word smooth introduced only because the surface or the curve given by.

A function can therefore be said to be smooth over. For an algebraic curve of degree n, with , the curve is smooth in the real (resp. Smooth functions ' graphs, as seen under sufficient magnification, are approximated by their tangents.

Smooth point of a function). Smooth manifold, a differentiable manifold for which all the transition. A smooth function must be differentiable, and the derivative must be continuous.

According to wikipedia, a smooth function is a function that has derivatives of all orders. In mathematics, a smooth maximum of an indexed family x 1,., x n of numbers is a smooth approximation to the maximum function (,.,), meaning a parametric family of. The modification of a set of data to make it smooth and nearly continuous and remove or diminish outlying points.

The aim of smoothing is to give a general idea of relatively slow changes of value with little attention paid to the close matching of data values, while curve fitting concentrates on. In other words, they are continuous, differentiable, and so. Graphically, a smooth function of a single variable can be plotted as a single.

A function is sufficiently smooth if it is differentiable sufficient number of times. In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. A function for which each value of the argument is a smooth point (cf.

This adaptive behavior transforms the algorithm into one that effectively solves smooth problems after a few iterations, setting our work apart from existing iteratively. A smooth function is a function that has continuous derivatives up to some desired order over some domain. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the.